札记之PHP实现AVL树(平衡二叉树)

Posted on | In

定义：

一棵AVL树需要满足以下的条件:

  • 它的左子树和右子树都是AVL树。
  • 左子树和右子树的高度差不能超过1。

性质:

  • 一棵n个节点的AVL树的其高度保持在O(log2(n))。
  • 一棵n个节点的AVL树的平均搜索长度保持在O(log2(n))。
  • 一棵n个节点的AVL树删除一个结点做平衡化旋转所需要的时间为O(log2(n))。

设计与实现:

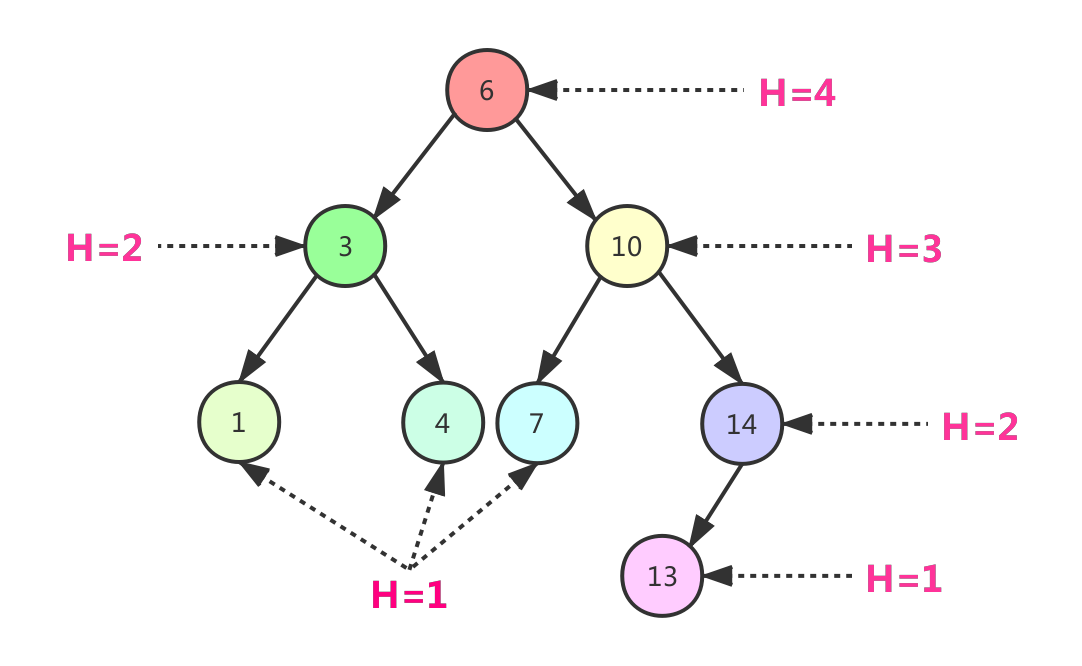
高度
  • 注：空节点高度为0，叶子节点的高度为1，根节点的高度最大;
    札记之PHP实现AVL树
1
2
3
4
5
6
7
8
9
public function height($node) 
{
    if ($node == null) {
        return null;
    }
    $leftHeight = $this->height($node->left);
    $rightHeight = $this->height($node->right);
    return 1 + max($leftHeight, $rightHeight);
}
旋转

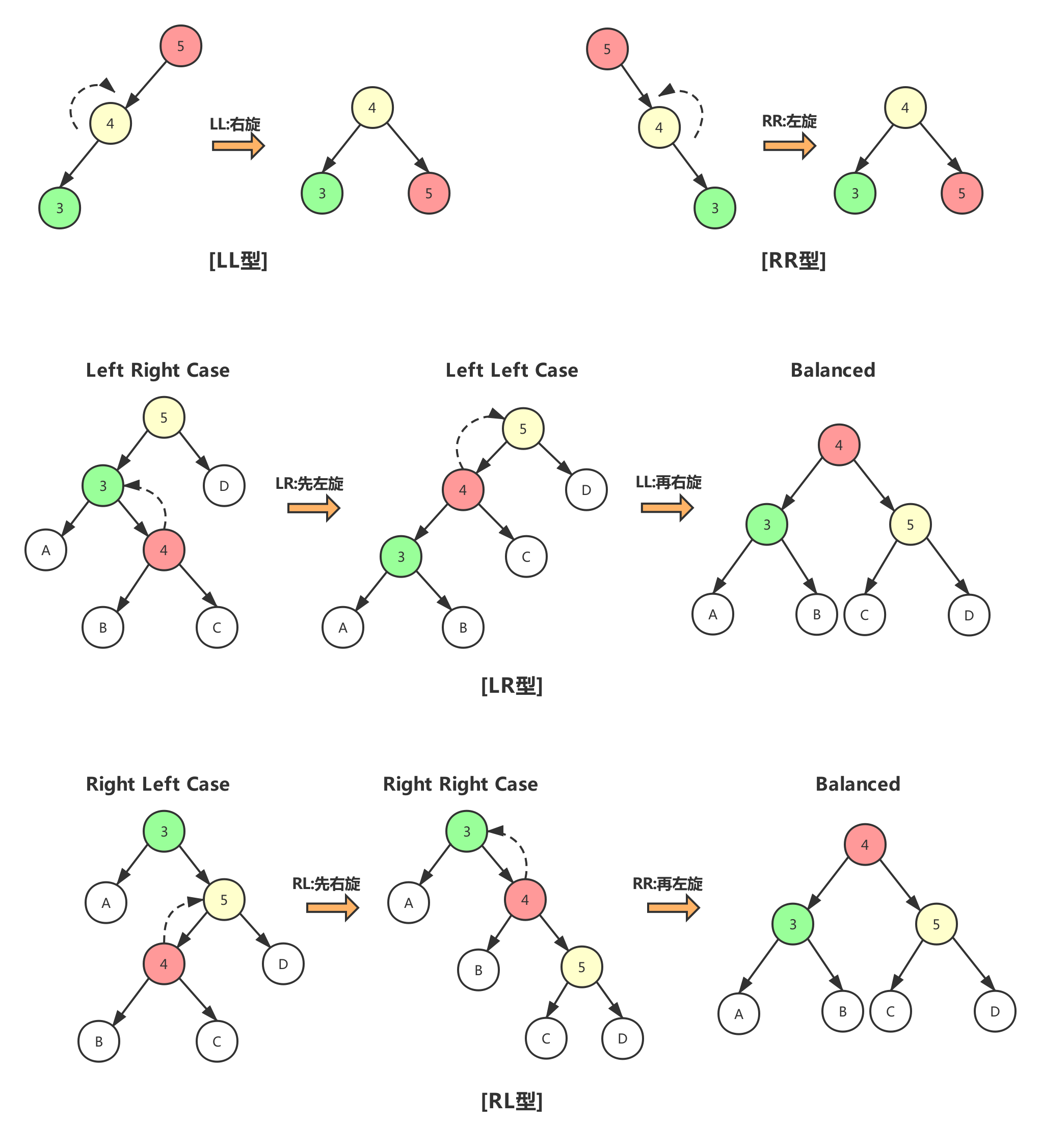
在新插入节点时，可能会破坏树的平衡性，这时需要利用旋转节点之间的链接关系来调整使之平衡

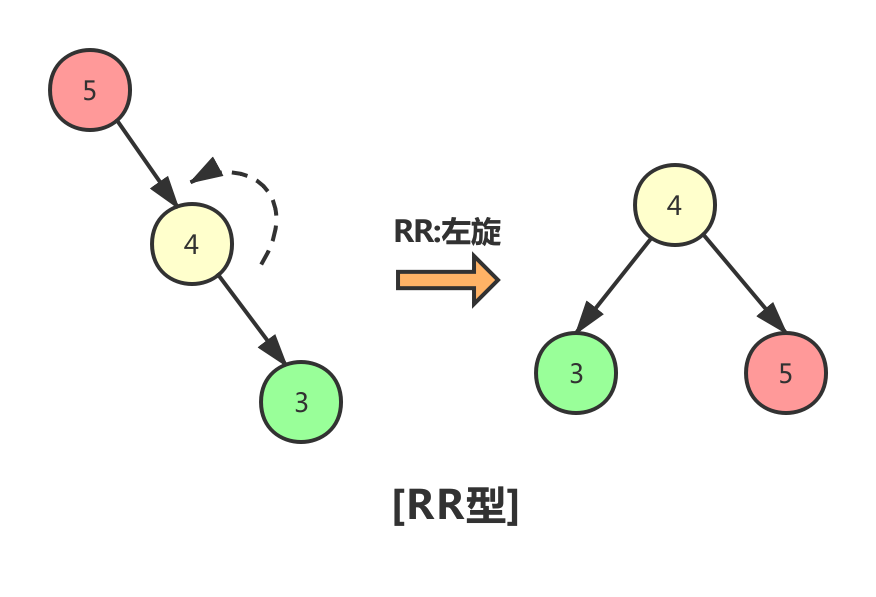
  • RR型：调整方式为直接左旋：失衡根节点作旋转节点左孩子即可。
    札记之PHP实现AVL树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public function leftRotate(&$node) 
{
    //创建新的结点，以当前根结点的值
    $newNode = new Node($node->data);

    //把新的结点的左子树设置成当前结点的左子树
    $newNode->left = $node->left; 

    //把新的结点的右子树设置成带你过去结点的右子树的左子树 
    $newNode->right = $node->right->left;

    //把当前结点的值替换成右子结点的值
    $node->data = $node->right->data;

    //把当前结点的右子树设置成当前结点右子树的右子树
    $node->right = $node->right->right;

    //把当前结点的左子树(左子结点)设置成新的结点
    $node->left = $newNode;
}
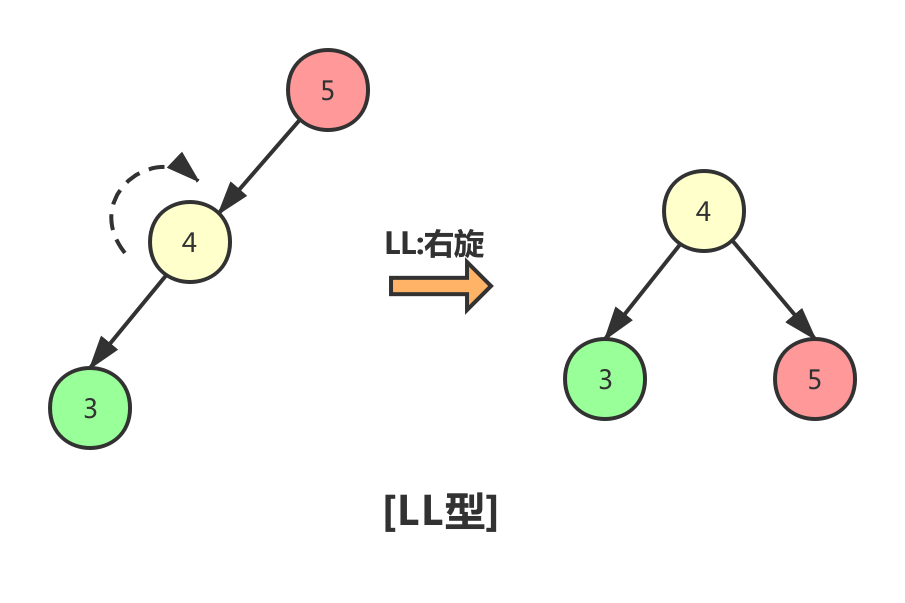
  • LL型：调整方式为直接右旋：失衡根节点作旋转节点右孩子即可。
    札记之PHP实现AVL树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//[LL型：右旋转]
public function rightRotate(&$node) 
{
    //创建新的结点，以当前根结点的值
    $newNode = new Node($node->data); 
   
    //把新的结点的右子树设置成当前结点的右子树
    $newNode->right = $node->right;

    //把新的结点的左子树设置成带你过去结点的左子树的右子树  
    $newNode->left = $node->left->right;

    //把当前结点的值替换成左子结点的值
    $node->data = $node->left->data;

    //把当前结点的左子树设置成当前结点左子树的左子树
    $node->left = $node->left->left;

    //把当前结点的右子树(右子结点)设置成新的结点
    $node->right = $newNode; 
}
  • RL型：这种情况下单一左旋转不能满足二叉查找树特性要求，因此，需要先右旋转换为RR型，然后再左旋以满足平衡条件
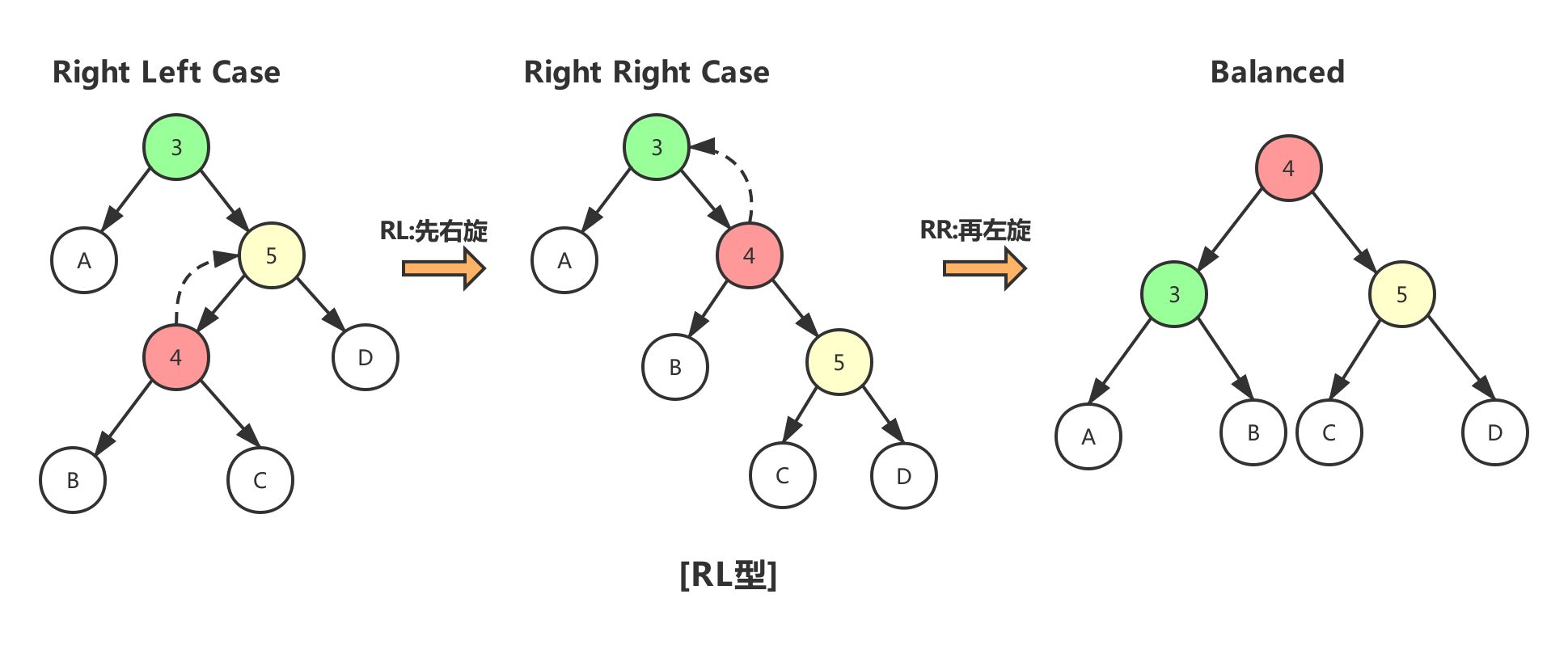
    札记之PHP实现AVL树
1
2
3
4
5
6
7
8
9
//[RL型：右旋-左旋]
public function rightLeftRotate(&$node)
{
    //先对右子结点进行右旋转 
    $this->rightRotate($node->right);

    //然后在对当前结点进行左旋转
    $this->leftRotate($node);
}
  • LR型：该情况与RL型是对称的
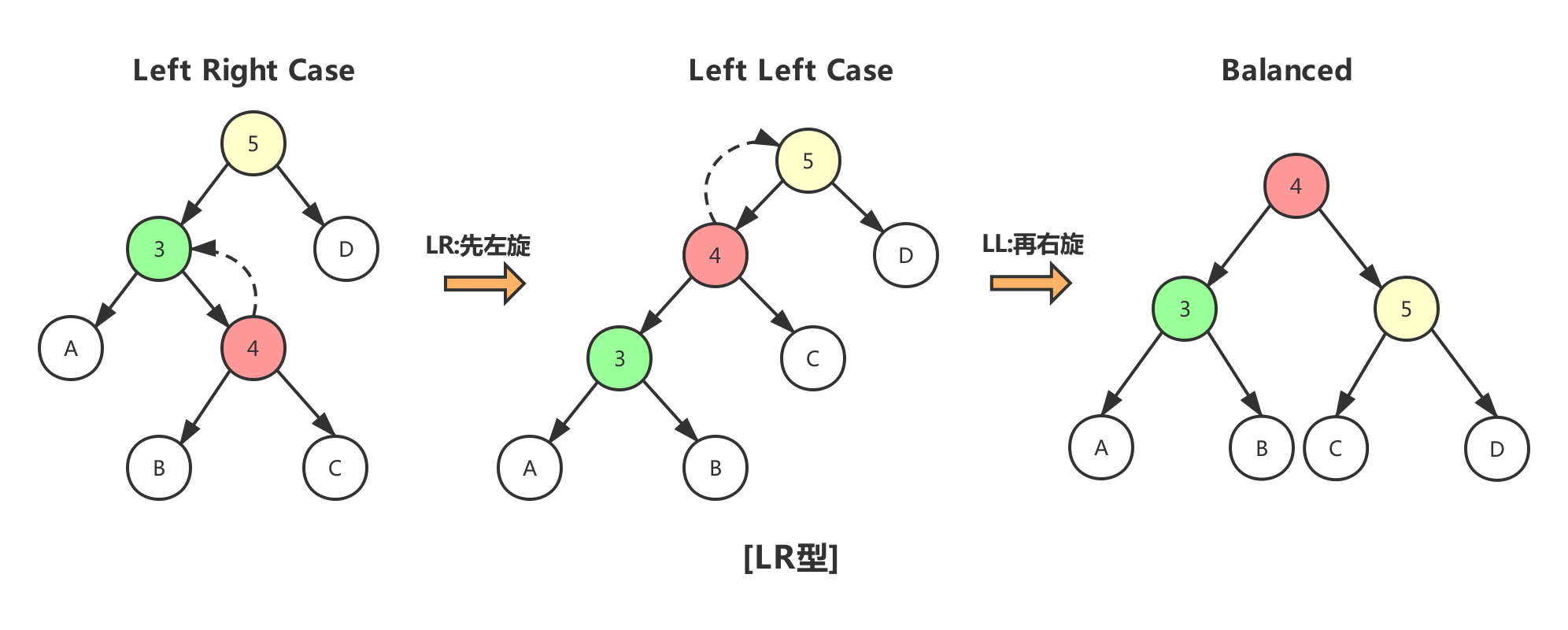
    札记之PHP实现AVL树
1
2
3
4
5
6
7
8
9
//[LR型：左旋-右旋]
public function leftRightRotate(&$node)
{
    //先对当前结点的左结点(左子树)->左旋转 
    $this->leftRotate($node->left);

    //再对当前结点进行右旋转
    $this->rightRotate($node);
}

PHP代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
class Node 
{
    public $left;
    public $right;
    public $data;

    public function __construct($data) 
    {
        $this->data = $data;
        $this->left = null;
        $this->right = null;
    }
}

class BinaryTree
{
    public $root = null;
 
    //插入节点
    public function insert($data)
    {
        $newNode = new Node($data);
        if ($this->root == null) {
            $this->root = $newNode;
        } else {
            $this->insertNode($this->root, $newNode);
        }
    }

    private function insertNode($node, $newNode) 
    {
        if ($newNode->data < $node->data) {
            if ($node->left == null) {
                $node->left = $newNode;
            } else {
                $this->insertNode($node->left, $newNode);
            }
            //当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
            if ($this->height($node->left) - $this->height($node->right) > 1) {
                //如果它的左子树的右子树高度大于它的左子树的高度
                if ($node->left != null && $this->height($node->left->right) > $this->height($node->left->left)) {
                    //LR型：左旋-右旋
                    $this->leftRightRotate($node);
                } else { 
                    //LL型：右旋转
                    $this->rightRotate($node);
                } 
            }
        } else {
            if ($node->right == null) {
                $node->right = $newNode;
            } else {
                $this->insertNode($node->right, $newNode);
            }
            //当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1, 左旋转
            if ($this->height($node->right) - $this->height($node->left) > 1) {
                //如果它的右子树的左子树的高度大于它的右子树的右子树的高度 
                if ($node->right != null && $this->height($node->right->left) > $this->height($node->right->right)) {
                    //RL型：右旋-左旋
                    $this->rightLeftRotate($node);
                } else { 
                    //RR型：左旋转
                    $this->leftRotate($node);
                }
            }
        }
    }

    public function height($node) 
    {
        if ($node == null) {
            return null;
        }
        $leftHeight = $this->height($node->left);
        $rightHeight = $this->height($node->right);
        return 1 + max($leftHeight, $rightHeight);
    }

    //[RR型：左旋转]
   public function leftRotate(&$node) 
   {
        //创建新的结点，以当前根结点的值
        $newNode = new Node($node->data);

        //把新的结点的左子树设置成当前结点的左子树
        $newNode->left = $node->left; 

        //把新的结点的右子树设置成带你过去结点的右子树的左子树 
        $newNode->right = $node->right->left;

        //把当前结点的值替换成右子结点的值
        $node->data = $node->right->data;

        //把当前结点的右子树设置成当前结点右子树的右子树
        $node->right = $node->right->right;

        //把当前结点的左子树(左子结点)设置成新的结点
        $node->left = $newNode;
    }

    //[LL型：右旋转]
    public function rightRotate(&$node) 
    {
        //创建新的结点，以当前根结点的值
        $newNode = new Node($node->data); 
       
        //把新的结点的右子树设置成当前结点的右子树
        $newNode->right = $node->right;

        //把新的结点的左子树设置成带你过去结点的左子树的右子树  
        $newNode->left = $node->left->right;

        //把当前结点的值替换成左子结点的值
        $node->data = $node->left->data;

        //把当前结点的左子树设置成当前结点左子树的左子树
        $node->left = $node->left->left;

        //把当前结点的右子树(右子结点)设置成新的结点
        $node->right = $newNode; 
    }

    //[RL型：右旋-左旋]
    public function rightLeftRotate(&$node)
    {
        //先对右子结点进行右旋转 
        $this->rightRotate($node->right);
        //然后在对当前结点进行左旋转
        $this->leftRotate($node);
    } 

    //[LR型：左旋-右旋]
    public function leftRightRotate(&$node)
    {
        //先对当前结点的左结点(左子树)->左旋转 
        $this->leftRotate($node->left);
        //再对当前结点进行右旋转
        $this->rightRotate($node);
    }

    function isBalanced($node) 
    {
        return abs($this->leftHeight($node) - $this->rightHeight($node)) < 2;
    }

    function rightHeight($node)
    {
        if ($node->right == null) {
            return 0;
        }
        return $this->rightHeight($node->right)+1;
    }

    function leftHeight($node)
    {
        if ($node->left == null) {
            return 0;
        }
        return $this->leftHeight($node->left)+1;
    }
    
    //查询
    public function search($data)
    {
        if ($node == null) {
            return null;
        }
        return $this->searchNode($this->root, $data);
    }

    private function searchNode($node, $data)
    {
        if ($node == null) {
            return false;
        }
        if ($data < $node->data) {
            return $this->searchNode($node->left, $data);
        } else if ($data > $node->data) {
            return $this->searchNode($node->right, $data);
        } else {
            return $node;
        }
    }

    //删除
    public function delete($data)
    {
        $node = $this->deleteNode($this->root, $data);
    }

    public function deleteNode($node, $data)
    {
        if ($node == null) {
            return null;
        }

        if ($data < $node->data) {
            $node->left = $this->deleteNode($node->left, $data);
            if ($this->height($node->right) - $this->height($node->left) > 1) {
                $currentNode = $node->right;
                if ($node->right != null && $this->height($currentNode->left) > $this->height($currentNode->right)) {
                    //RL型：右旋-左旋
                    $currentNode = $this->rightLeftRotate($node);
                } else { 
                    //RR型：左旋转
                    $currentNode = $this->leftRotate($node);
                }
            }
        } else if ($data > $node->data) {
            $node->right = $this->deleteNode($node->right, $data);
            if ($this->height($node->left) - $this->height($node->right) > 1) {
                $currentNode = $node->left;
                if ($node->left != null && $this->height($currentNode->right) > $this->height($currentNode->left)) {
                    //LR型：左旋-右旋
                    $currentNode = $this->leftRightRotate($node); 
                } else { 
                    //LL型：右旋转
                    $currentNode = $this->rightRotate($node);
                } 
            }
        } else {
            if ($node->left == null && $node->right == null) {
                $node = null;
            } else if ($node->left == null) {
                $node = $node->right;
            } else if ($node->right == null) {
                $node = $node->left;
            } else {
                //找出要删除的节点，用他左边子节点去替换要删除的节点
                $aux = $this->findMinNode($node->right);
                $node->data = $aux->data;
                $node->right = $this->deleteNode($node->right, $aux->data);
            }
        }
        return $node;
    }

    //找出左侧最小节点
    private function findMinNode($node)
    {
        if ($node == null) {
            return null;
        }
        while ($node && $node->left != null) {
            $node = $node->left;
        }
        return $node;
    }

    public function min()
    {
        return $this->minNode($this->root);
    }

    //找出左侧最小节点
    private function minNode($node)
    {
        if ($node == null) {
            return null;
        }
        while ($node && $node->left != null) {
            $node = $node->left;
        }
        return $node->data;
    }

    public function max()
    {
        return $this->maxNode($this->root);
    }

    //找出右侧最大节点值
    private function maxNode($node)
    {
        if ($node == null) {
            return null;
        }
        while ($node && $node->right != null) {
                $node = $node->right;
        }
        return $node->data;
    }

    //层数
    public function getHeight($node)
    {
        if ($node == null) {
            return null;
        }
        $leftH = $this->getHeight($node->left);
        $rightH = $this->getHeight($node->right);

        return max($leftH, $rightH) + 1;
    }

    //前序遍历
    public function preOrder($node)
    {
        if ($node == null) {
            return ;            
        }
        echo $node->data . '->';
        $this->preOrder($node->left);
        $this->preOrder($node->right);
    }

    //中序遍历
    public function inOrder($node)
    {
        if ($node == null) {
            return ;            
        }
        $this->inOrder($node->left);
        echo $node->data . '->';
        $this->inOrder($node->right);
    }

    //后序遍历
    public function postOrder($node)
    {
        if ($node == null) {
            return ;            
        }
        $this->postOrder($node->left);
        $this->postOrder($node->right);
        echo $node->data . '->';
    }
}    

$nodes = [10, 20, 7, 17, 18, 22, 23, 24, 25];
$avlObj = new BinaryTree();

foreach ($nodes as $node) {
    $avlObj->insert($node);
}

printf("中序遍历\n");
$avlObj->inOrder($avlObj->root);
echo PHP_EOL;

$avlObj->delete(20);

printf("删除后中序遍历！\n");
$avlObj->inOrder($avlObj->root);

printf("层数: %d\n", $avlObj->rightHeight($avlObj->root));

printf("平衡因子: %d\n",$avlObj->isBalanced($avlObj->root));

printf("右子树高度: %d\n", $avlObj->rightHeight($avlObj->root));

printf("左子树高度: %d\n", $avlObj->leftHeight($avlObj->root));

运行结果

1
2
3
4
5
6
7
8
中序遍历
7->10->17->18->20->22->23->24->25->
删除后中序遍历！
7->10->17->18->22->23->24->25->
层数: 2
平衡因子: 1
右子树高度: 2
左子树高度: 2

全图展示

札记之PHP实现AVL树

-------------本文结束感谢您的阅读-------------
坚持原创技术分享，您的支持将鼓励我继续创作！