札记之PHP实现Dijkstra算法[广度搜索]

上一篇采用的是优先队列实现，这篇用广度搜索实现，从图示+代码层更好理解了

图示

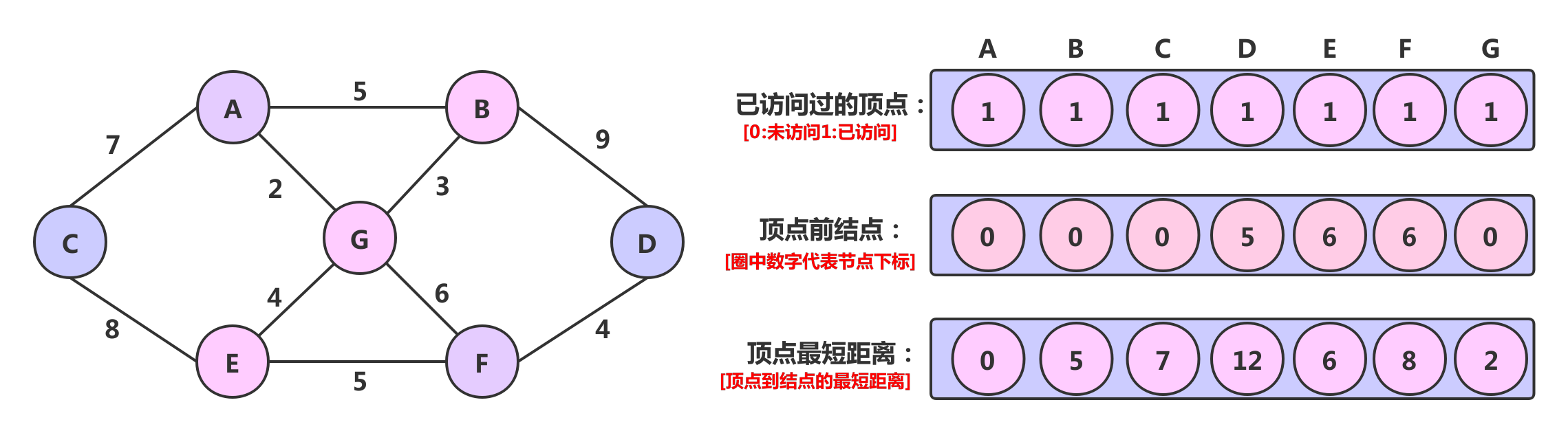
算法思路

定义三个数组

• $visited: 记录各个顶点是否访问过1表示访问过,0未访问;
• $preVisited: 每个下标对应的值为前一个顶点下标[可以访问到任何顶点的最短路径];
• $distance: 记录出发顶点到其他所有顶点的距离;

  比如G为出发顶点，就会记录G到其它顶点的距离，会动态更新，求的最短距离就会存放到distance

算法过程

• 设置出发顶点为v，顶点集合V{v1,v2,vi…}，v到V中各顶点的距离构成距离集合Dis，Dis{d1,d2,di…}，Dis 集合记录着 v 到图中各顶点的距离(到自身可以看作 0，v到 vi 距离对应为 di)
• 从Dis中选择值最小的di并移出Dis集合，同时移出V集合中对应的顶点vi，此时的v到vi为最短路径
• 更新Dis集合，更新规则为:比较v到V集合中顶点的距离值，与v通过vi到V集合中顶点的距离值，保留值较小的一个(同时也应该更新顶点的前驱节点为 vi，表明是通过 vi 到达的)
• 重复执行两步骤，直到最短路径顶点为目标顶点即可结束

PHP代码实现

class Graph
{
    private $vertex = [];
    private $martrix = [];
    private $vv;

    public function __construct($vertex, $martrix)
    {
        $this->vertex = $vertex;
        $this->martrix = $martrix;
    }

    public function showGraph()
    {
        foreach ($this->martrix as $vertex => $link) {
            printf("顶点为：%d\n", $vertex);
            var_dump('对应关系：', $link);
        }
    }

    public function showDijkstra() 
    {
        $this->vv->show(); 
    }

    public function djs($index) 
    {
        $this->vv = new VisitedVertex(count($this->vertex), $index);
        //更新 $index 顶点到周围顶点的距离和前驱顶点 
        $this->update($index);
        for ($j = 1; $j < count($this->vertex); $j++) {
            //选择并返回新的访问顶点
            $index = $this->vv->updateArr();
            //更新index顶点到周围顶点的距离和前驱顶点
            $this->update($index);
        }
    }

    public function pathsTo($toNode) 
    {
        $path = array();
        $current = $toNode;    
        $nodeDistance = $this->vv->preVisited;
        if (isset($nodeDistance[$current])) {
            array_push($path, $toNode);
        }
      
        while (isset($nodeDistance[$current])) {
            $nextnode = $nodeDistance[$current];
            array_push($path, $nextnode);
            if ($nextnode == 0) {
                break;
            }
            $current = $nextnode;
        }
        return array_reverse($path);
    }

    //更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点,
    public function update($index) 
    {
        $len = 0;
        //根据遍历我们的邻接矩阵的 matrix[index]行 
        $martrixLength = count($this->martrix[$index]);
        for ($j = 0; $j < $martrixLength; $j++) {
            // len 含义是 : 出发顶点到 index 顶点的距离 + 从 index 顶点到 j 顶点的距离的和 
            $len = $this->vv->getDistance($index) + $this->martrix[$index][$j];
            // 如果 j 顶点没有被访问过，并且 len 小于出发顶点到 j 顶点的距离，就需要更新 
            if (!$this->vv->in($j) && $len < $this->vv->getDistance($j)) {
                //更新 j 顶点的前驱为 index 顶点
                $this->vv->updatePre($j, $index);
                //更新出发顶点到 j 顶点的距离 
                $this->vv->updateDis($j, $len); 
            }
        } 
    }
}

// 已访问顶点集合 
class VisitedVertex 
{
    // 记录各个顶点是否访问过 1 表示访问过,0 未访问,会动态更新
    public $visited;
    // 每个下标对应的值为前一个顶点下标, 会动态更新
    public $preVisited;
    // 记录出发顶点到其他所有顶点的距离,
    public $distance;

    public function __construct($length, $index)
    {   
        //初始化数组
        $this->visited = array_fill(0, $length, 0); 
        $this->preVisited = array_fill(0, $length, 0);
        $this->distance = array_fill(0, $length, N); 

        //设置出发顶点被访问过
        $this->visited[$index] = 1; 
        //设置出发顶点的访问距离为 0
        $this->distance[$index] = 0;
    }

    public function in($index) 
    {
        return $this->visited[$index] == 1; 
    }

    public function updateDis($index, $len) 
    {
        $this->distance[$index] = $len;
    }

    public function updatePre($pre, $index)
    { 
        $this->preVisited[$pre] = $index;
    }

    public function getDistance($index) 
    { 
        return $this->distance[$index];
    }

    public function updateArr() 
    {
        $min = N;
        $index = 0;
        $visitedNum = count($this->visited);
        for ($i = 0; $i < $visitedNum; $i++) {
            if ($this->visited[$i] == 0 && $this->distance[$i] < $min) { 
                $min = $this->distance[$i];
                $index = $i; 
            }
        }
        //更新 index 顶点被访问过 
        $this->visited[$index] = 1; 
        return $index;
    }

    public function show() 
    {
        print "已访问过的顶点:\n\r";
        print_r($this->visited);
        print "顶点前缀结点:\n\r";
        print_r($this->preVisited);
        print "顶点最短距离:\n\r";
        print_r($this->distance);
    }
}

define("N", INF);
class DijkstraAlgorithm
{
    function createGraph()
    {
        $vertex = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
        $matrix[0] = [N, 5, 7, N, N, N, 2];
        $matrix[1] = [5, N, N, 9, N, N, 3];
        $matrix[2] = [7, N, N, N, 8, N, N];
        $matrix[3] = [N, 9, N, N, N, 4, N];
        $matrix[4] = [N, N, 8, N, N, 5, 4];
        $matrix[5] = [N, N, N, 4, 5, N, 6];
        $matrix[6] = [2, 3, N, N, 4, 6, N];

        $GraphObj = new Graph($vertex, $matrix);
        $GraphObj->djs(0);
        $GraphObj->showDijkstra();
        $path = $GraphObj->pathsTo('3');

        print '[A->C]最短路径为：';
        foreach ($path as $node) {
            printf("%s===>", $vertex[$node]);
        }
    }
}
$Dijkstra = new DijkstraAlgorithm();
$Dijkstra->createGraph();

运行结果

已访问过的顶点:
Array
(
    [0] => 1
    [1] => 1
    [2] => 1
    [3] => 1
    [4] => 1
    [5] => 1
    [6] => 1
)
顶点前结点:
Array
(
    [0] => 0
    [1] => 0
    [2] => 0
    [3] => 5
    [4] => 6
    [5] => 6
    [6] => 0
)
顶点到各顶点最短距离:
Array
(
    [0] => 0
    [1] => 5
    [2] => 7
    [3] => 12
    [4] => 6
    [5] => 8
    [6] => 2
)
[A->D]最短路径为：
A===>G===>F===>D