札记之PHP实现图的广度优先遍历(BFS)

基本思想

• 从图中的某个顶点V出发访问并记录；
• 依次访问顶点V的邻接顶点w1、w2……wk；
• 分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，直到图中所有已被访问过的顶点的邻接点都被访问到；
• 重复第3步，直到图中所有顶点都被访问完为止。

存储结构

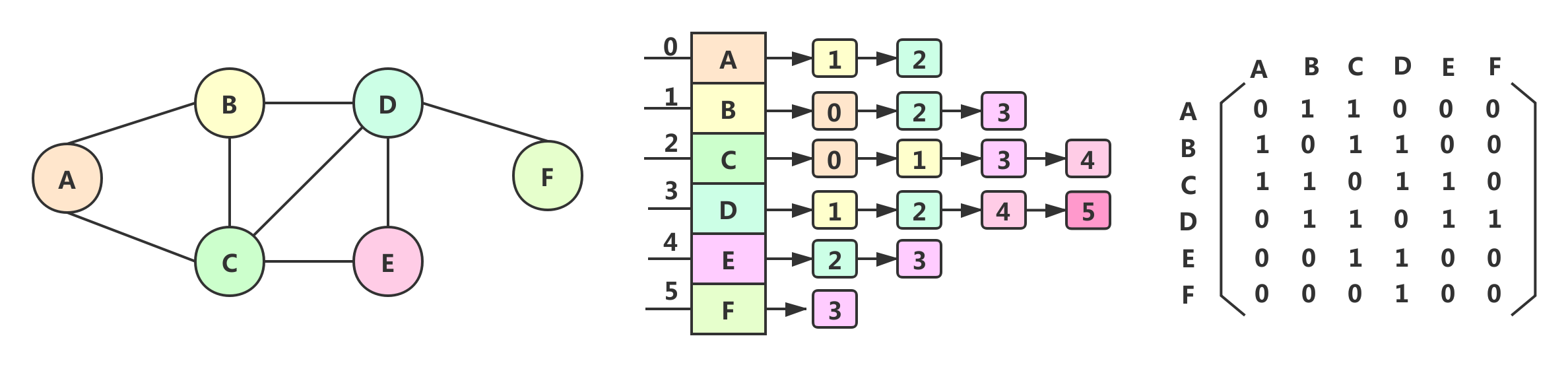
实现方式

邻接表非递归实现

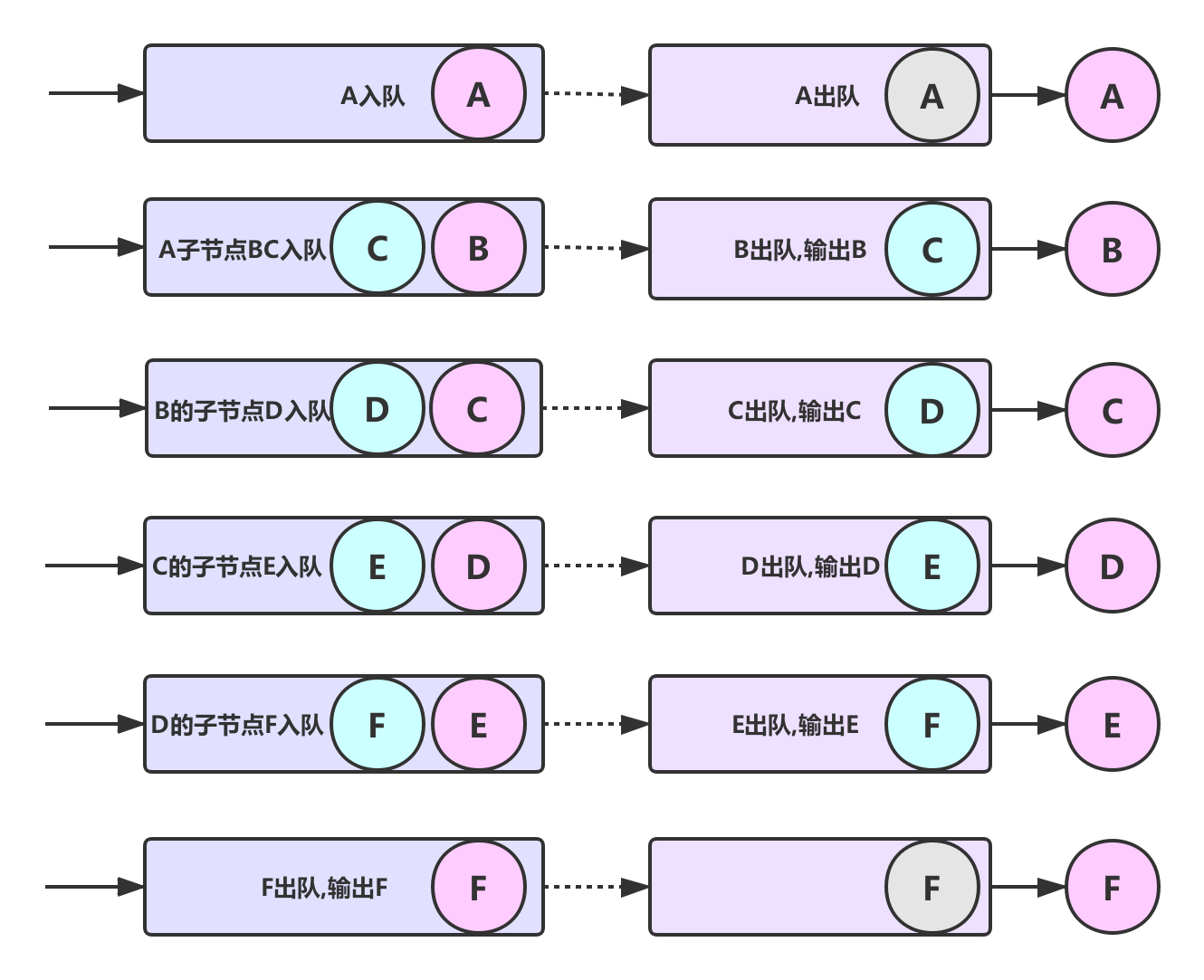
广度优先算法：采用队列（先进先出FIFO）的思想，遍历节点时，被遍历的节点出队列，再遍历其子节点，如下所示

对照上图看队列的变化

邻接表非递归实现

class Node
{
    public $value = null;
    public $next = array();//存储下一个节点位置的数组

    public function __construct($value = null) 
    {
        $this->value = $value;
    }
}

class Graph 
{
    // 记录已被遍历节点
    public $visited = [];
    // 图的邻接表数组
    public $graph = [];

    /**
     * 为顶点添加邻接点
     * @param $vertex 顶点v
     * @param $adjvex 顶点v的邻接点
     */
    public function addVertex($vertex, $adjvex)
    {
        $this->graph[$vertex][] = $adjvex;
    }

    /**
     * 非递归
     * @param $v 传入的是第一个需要访问的顶点
     */
    public function BFS($v)
    {
        // 初始化节点遍历标记
        $vertices = array_keys($this->graph);
        foreach ($vertices as $vertex) {
            $this->visited[$vertex] = 0;
        }

        $queue = [];
        $this->visited[$v] = 1;
        // 初始化顶点入队列            
        array_push($queue, $v);

        while (!empty($queue)) {                
            $current = array_shift($queue);
            echo $current . PHP_EOL;
            // 查找相邻节点
            foreach ($this->graph[$current] as $curChildNode) {
                if ($this->visited[$curChildNode] == 0) {
                    //将找到的此顶点入队列 
                    array_push($queue, $curChildNode);
                    //将找到的此顶点标记为已访问
                    $this->visited[$curChildNode] = 1;
                }
            }
        }
    }
}

$vertices = ['a', 'b', 'c', 'd', 'e', 'f'];
$graph = new Graph();
$graph->addVertex('a', 'b');
$graph->addVertex('a', 'c');
$graph->addVertex('b', 'a');
$graph->addVertex('b', 'c');
$graph->addVertex('b', 'd');
$graph->addVertex('c', 'a');
$graph->addVertex('c', 'b');
$graph->addVertex('c', 'd');
$graph->addVertex('c', 'e');
$graph->addVertex('d', 'b');
$graph->addVertex('d', 'c');
$graph->addVertex('d', 'e');
$graph->addVertex('d', 'f');
$graph->addVertex('e', 'd');
$graph->addVertex('e', 'c');
$graph->addVertex('f', 'd');
$graph->BFS('a');

结果

a
b
c
d
e
f

邻接矩阵非递归实现

class Graph 
{
    // 存储节点信息
    public $vertices;
    // 存储边信息
    public $arcs;
    // 图的节点数
    public $vexnum;
    // 记录节点是否已被遍历
    public $visited = [];

    // 初始化
    public function __construct($vertices) 
    {
        $this->vertices = $vertices;
        $this->vexnum = count($this->vertices);
        for ($i = 0; $i < $this->vexnum; $i++) {
            for ($j = 0; $j < $this->vexnum; $j++) {
                $this->arcs[$i][$j] = 0;
            }
        }
    }
 
    // 两个顶点间添加边(无向图)
    public function addEdge($a, $b)
    {
        // 边的头尾不能为同一节点
        if ($a == $b) {
            return;
        }
        $this->arcs[$a][$b] = 1;
        $this->arcs[$b][$a] = 1;
    }

    // 非递归
    public function BFS()
    {
        // 初始化节点遍历标记
        for ($i = 0; $i < $this->vexnum; $i++) {
            $this->visited[$i] = 0;
        }
      
        $queue = [];
        for ($i = 0; $i < $this->vexnum; $i++) {
            if (!$this->visited[$i]) {
                //记录初始顶点，入队列
                $this->visited[$i] = 1;
                echo $this->vertices[$i] . PHP_EOL;

                $queue[] = $i;             
                while (!empty($queue)) {
                    // 元素出队
                    $current = array_shift($queue);    
                    for ($j = 0; $j < $this->vexnum; $j++) {
                        if ($this->arcs[$current][$j] == 1 && $this->visited[$j] == 0) {
                            // 将找到的此顶点标记为已访问
                            $this->visited[$j] = 1;
                            echo $this->vertices[$j] . PHP_EOL;
                             // 将找到的此顶点入队列
                            $queue[] = $j;         
                        }
                    }
                }
            }
        }
    }
}

$vertices = ['a', 'b', 'c', 'd', 'e', 'f'];
$graph = new Graph($vertices);

$graph->addEdge('a', 'b');
$graph->addEdge('a', 'c');
$graph->addEdge('b', 'a');
$graph->addEdge('b', 'c');
$graph->addEdge('b', 'd');
$graph->addEdge('c', 'a');
$graph->addEdge('c', 'b');
$graph->addEdge('c', 'd');
$graph->addEdge('c', 'e');
$graph->addEdge('d', 'b');
$graph->addEdge('d', 'c');
$graph->addEdge('d', 'e');
$graph->addEdge('d', 'f');
$graph->addEdge('e', 'd');
$graph->addEdge('e', 'c');
$graph->addEdge('f', 'd');
$graph->BFS();

结果

a
b
c
d
e
f