图(graph)由边(edge)的集合及顶点(vertex)的集合组成。通常记为:G=(V,E)。
图的概念
图
- 图(graph)由边(edge)的集合及顶点(vertex)的集合组成。通常记为:G=(V,E)。
有向图
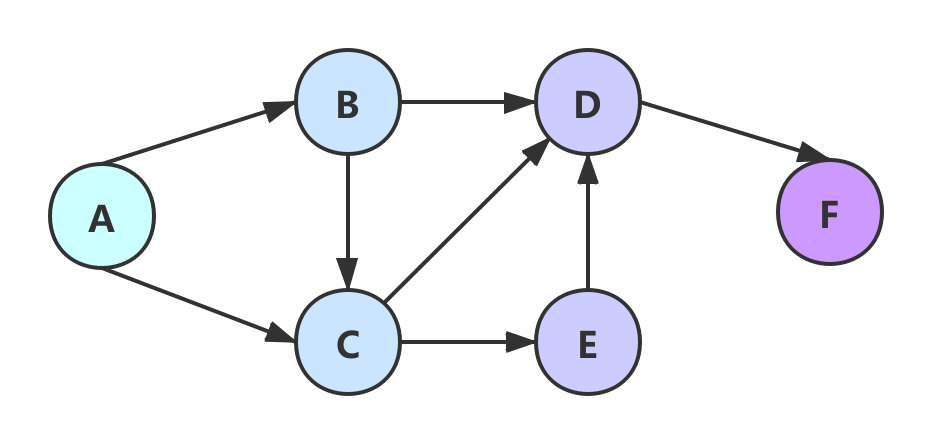
说明
- G=(V1,{E1}),其中:
- V1={A, B, C, D, E, F},V1表示由”A,B,C,D,E,F”几个顶点组成的集合。
- E1={<A, B>, <A, C>, <B, C>, <B, D>, <C, D>, <C, E>, <D, F>}。E1是由矢量<A,B>,矢量<A,C>…等组成的集合。其中,<A,C>表示由顶点A指向顶点C的有向边。
无向图
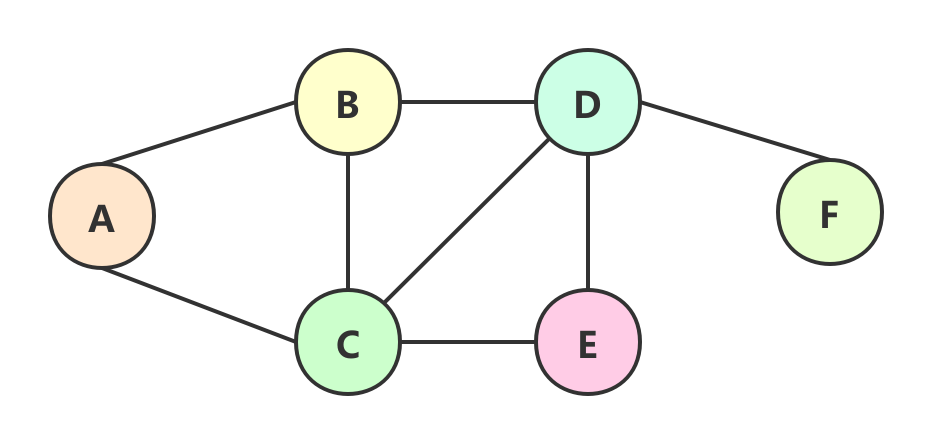
说明
- G=(V2,{E2}),其中:
- V2={A, B, C, D, E, F},V2表示由”A,B,C,D,E,F”几个顶点组成的集合。
- E2={(A, B), (A, C), (B, C), (B, D), (C, D), (C, E), (D, F)}。E2是由边(A,B),边(A,C)…等组成的集合。其中,(A,C)表示由顶点A和顶点C连接成的边。
顶点、邻接点、边、入边、出边
- 顶点:图中的元素我们就叫作顶点(vertex)
- 邻接点:一条边上的两个顶点叫做邻接点。
- 边:图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫作边(edge)。
- 入边:在有向图中,是指以该顶点为终点的边;
- 出边:在有向图中,指以该顶点为起点的边。
例如:
在上面的无向图中,顶点A和顶点B就是邻接点;
在上面的有向图中,<A, B>是A的出边、B的入边。
度
- 一个顶点的度是指与该顶点相关联的边的条数,顶点v的度记作d(v)。
- 对于有向图来说,一个顶点的度可细分为入度和出度。
- 入度:一个顶点的入度是指与其关联的各边之中,以其为终点的边数;
- 出度:出度则是相对的概念,指以该顶点为起点的边数。
例如:
在上面的无向图中,顶点A的度为2,顶点C的度为3,顶点D的度为4;
在上面的有向图中,顶点A的入度是0,出度是2;顶点B的入度是1,出度是2;顶点C的入度是2,出度是2。
图的存储结构(邻接矩阵,邻接表)
邻接矩阵 : 邻接矩阵是表示顶点之间相邻关系的矩阵。设图G有n个顶点,则邻接矩阵是一个n*n的方阵;
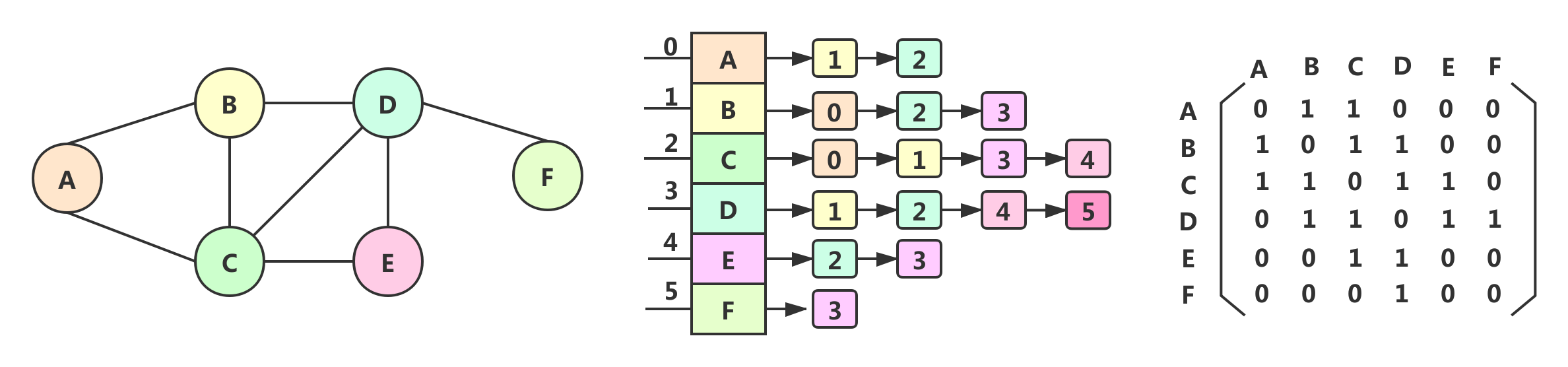
邻接矩阵代码
1 | class Graph |
邻接表: 当图中的边数较少时,用邻接矩阵来实现图结构会浪费很多内存空间,使用邻接表更省空间
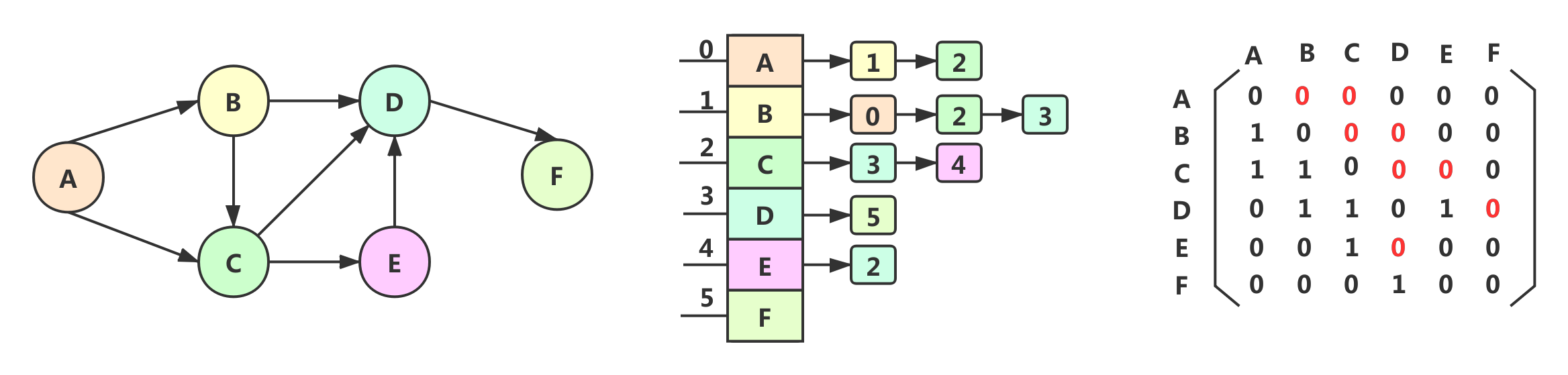
邻接表代码
1 | class Node |
图的遍历
深度优先遍历(Depth-First-Search, DFS)
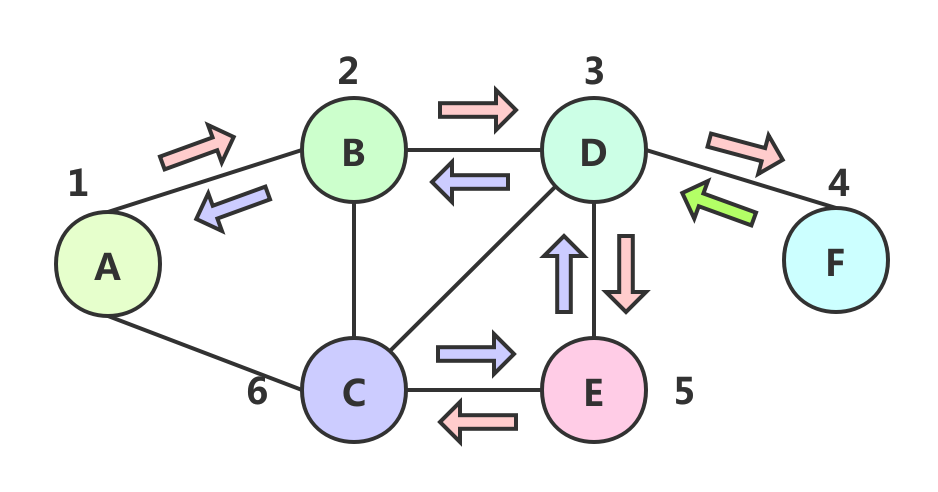
- 访问顶点v;
- 依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
- 若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
广度优先遍历(Breadth-First-Search, BFS)
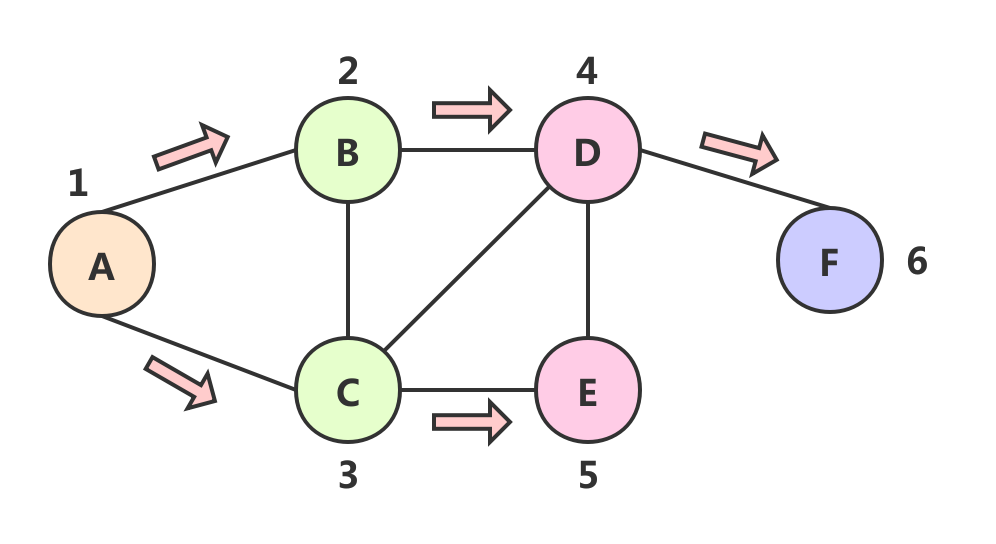
- 访问顶点vi;
- 访问vi的所有未被访问的邻接点w1 ,w2 , …wk;
- 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问。
