什么是二叉树搜索树:
二叉搜索树又被称为二叉排序树,那么它本身也是一棵二叉树,那么满足以下性质的二叉树就是二叉搜索树:
- 若左子树不为空,则左子树上左右节点的值都小于根节点的值
- 若它的右子树不为空,则它的右子树上所有的节点的值都大于根节点的值
- 它的左右子树也要分别是二叉搜索树
基于下图介绍二叉搜索树相关操作:
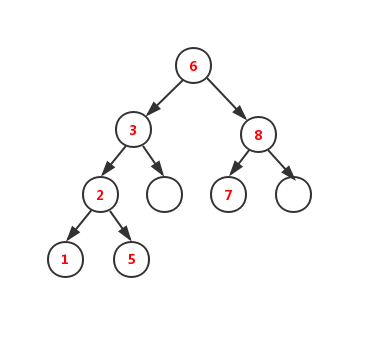
二叉搜索树的查找操作
- 我们先取根节点,如果它等于我们要查找的数据,那就返回;
- 如果要查找的数据比根节点的值小,那就在左子树中递归查找;
- 如果要查找的数据比根节点的值大,那就在右子树中递归查找;
二叉搜索树的插入操作
- 如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;
- 如果不为空,就再递归遍历右子树,查找插入位置;
- 如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;
二叉搜索树的删除操作
- 如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null;
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了;
- 如果要删除的节点有两个子节点,我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点;
二叉搜索树最小值
- 循环左侧节点,找对最小值;
二叉搜索树最大值
- 循环右侧节点,找对最大值;
获取层数
- 递归左右高度,取最大值+1;
完整代码:
1 | class Node |
结果:
1 | 先序遍历: |
