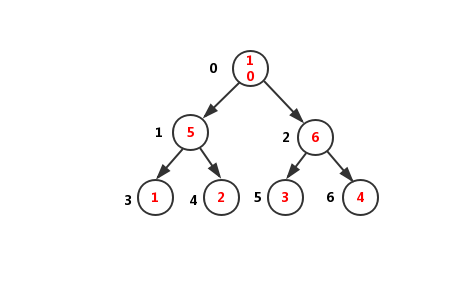
什么是树:
树(Tree)是n(n≥0)个结点的有限集;
树的概念:
- 节点的深度:节点到叶子节点的最长路径(边数);
- 节点的高度:根节点到这个节点所经历的边的个数;
- 节点的层数:节点的深度+1;
- 树的高度:根节点的高度;
如图所示:
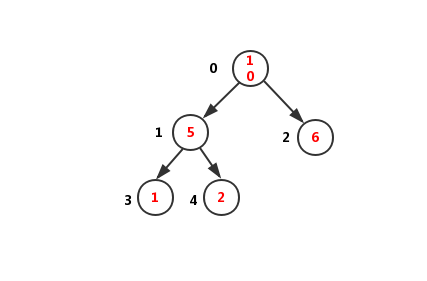
什么是二叉树(Binary Tree):
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree),同样的左右子树也都是二叉树.
它具有以下五种形态:
- 空树
- 仅有根结点
- 左子树为空
- 右子树为空
- 左右子树均非空
如图所示:
二叉树又分为满二叉树,完全二叉树;
满二叉树:
如图所示:
- 叶子节点全都在最底层,除了叶子节点之外;
- 高度为h,并且由2{h} –1个结点的二叉树,被称为满二叉树。
完全二叉树:
如图所示:
- 叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大;
二叉树性质总结:
- 二叉树的第 i 层上最多节点数 $$2^{i-1}$$
- 深度为 n 的二叉树,最多拥有的节点数 $$2^n-1$$
- 设满二叉树深度为 n,叶子结点数必为 $$2^{n-1}$$
二叉树的遍历:
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树;
- 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树;
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身;
如图所示: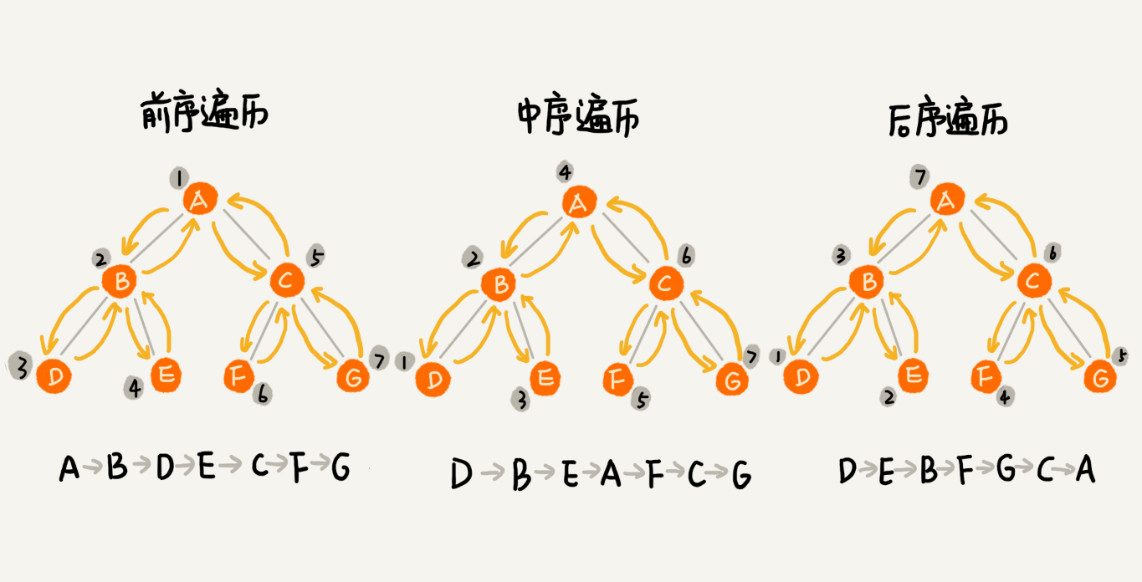
1 | 前序遍历的递推公式: |
完整代码: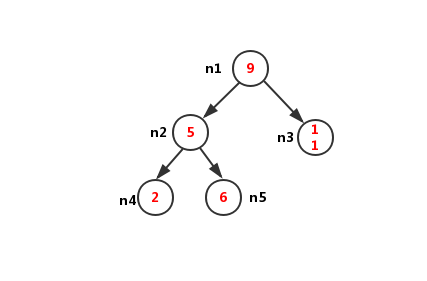
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
typedef struct node {
int data;
struct node* left;
struct node* right;
} Node;
//前序遍历(根->左->右)
void preOrder(Node* node) {
if (node == NULL) return;
printf("%d\n", node -> data);
preOrder(node -> left);
preOrder(node -> right);
}
//中序遍历(左->根->右)
void inOrder(Node* node) {
if (node == NULL) return;
inOrder(node -> left);
printf("%d\n", node -> data);
inOrder(node -> right);
}
//后序遍历(左->右->根)
void postOrder(Node* node) {
if (node == NULL) return;
postOrder(node -> left);
postOrder(node -> right);
printf("%d\n", node -> data);
}
int main() {
Node n1;
Node n2;
Node n3;
Node n4;
Node n5;
n1.data = 9;
n2.data = 5;
n3.data = 11;
n4.data = 2;
n4.data = 6;
n1.left = &n2;
n1.right = &n3;
n2.left = &n4;
n2.right = &n5;
n3.left = NULL;
n3.right = NULL;
n4.left = NULL;
n4.right = NULL;
n5.left = NULL;
n5.right = NULL;
printf("先序遍历!\n");
preOrder(&n1);
printf("中序遍历!\n");
inOrder(&n1);
printf("后序遍历!\n");
postOrder(&n1);
}
执行结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20jiayuandeMacBook-Pro:tree jiayuan$ gcc tree.c -o tree
jiayuandeMacBook-Pro:tree jiayuan$ ./tree
先序遍历!
9
5
2
6
11
中序遍历!
2
5
6
9
11
后序遍历!
2
6
5
11
9