PHP排序算法-堆排序(Heap Sort)

堆排序，英文名称 Heapsort，利用二叉树（堆）这种数据结构所设计的一种排序算法，是一种对直接选择排序的一种改建算法。在逻辑结构上是按照二叉树存储结构，正是这种结构优化了选择排序的性能，在物理存储上是连续的数组存储，它利用了数组的特点快速定位指定索引的元素。

什么是堆

• 结构性： 堆是一个完全二叉树，完全二叉树要求树的节点从左到右排列，除最后一层外，每层的节点个数都是满的。
• 堆序性： 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值，对于每个节点大于等于子节点值的堆称为大顶堆；每个节点小于等于子节点值的堆称为小顶堆;

堆的存储方式

完全二叉树比较适合用数组来存储，除根节点外，节点i的左子节点的下标为i2，右子节点的下标为i2+1，父节点的坐标为i/2，根节点没有父节点，下标为0的空间暂时用不到;

如图所示：

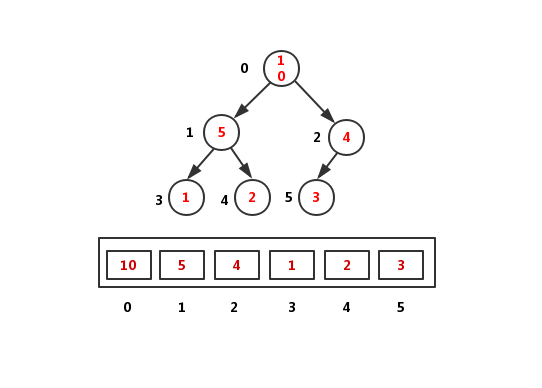
推出结论：

parentNo = (nodeNo) / 2
leftNo = parentNo * 2
rightNo = parentNo * 2 + 1
//-------example---------
$i = 3;
$parent = ($i-1) / 2; //1
$leftno =  2 * $i + 1 //3
$rightno = 2 * $i + 2 //4

堆的插入和删除

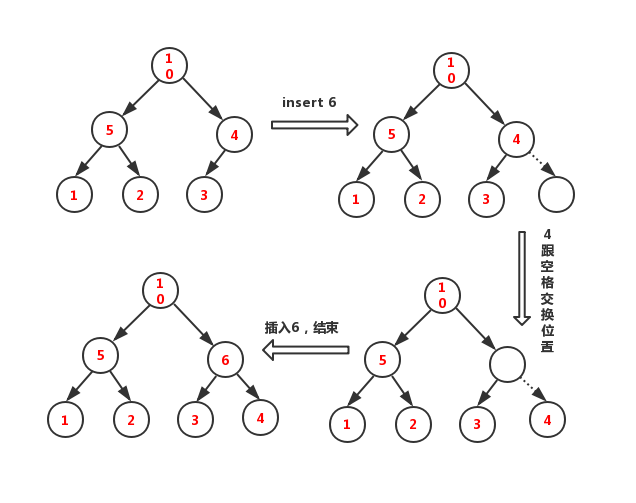
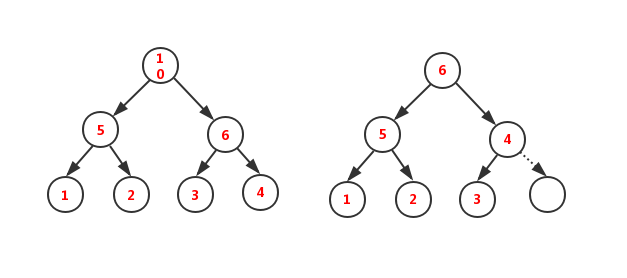
堆的插入和删除都要满足结构性和堆序性，比如插入一个新节点，该节点小于父节点值，则需要将该节点与父节点交换位置；递归此过程，直到重新满足堆序性为止；

插入（INSERT）

删除（Delete）

大顶堆排序代码实现

class MaxHeap
{
    function swap(&$arr, $i, $j) 
    {
        $temp = $arr[$i];
        $arr[$i] = $arr[$j];
        $arr[$j] = $temp;
    }
    //n：节点
    //i: 从哪个节点heapify
    function heapify(&$tree, $n, $i)
    {
        if ($i >= $n) {
            return; 
        }

        $c1 = (2 * $i) + 1;//左节点
        $c2 = (2 * $i) + 2;//右节点
        $max = $i;
   
        //左右节点内容跟父节点比较，确保父节点是最大值
        if ($c1 < $n && $tree[$c1] > $tree[$max]) {
            $max = $c1;
        }
        if ($c2 < $n && $tree[$c2] > $tree[$max]) {
            $max = $c2;
        }
        //当i是最大值时，不用交换
        if ($max != $i) {
            $this->swap($tree, $max, $i);
            //交换之后对下一层继续heapify
            $this->heapify($tree, $n, $max);
        }
    }

    //从下往上构建堆：节点3->节点2->节点1
    function buildHeap(&$tree, $n) 
    {
        $lastNode = $n - 1;
        $parent = ($lastNode - 1) / 2;
        for ($i = $parent; $i >= 0; $i--) {
            $this->heapify($tree, $n, $i);
        }
    }

    //堆排序(根节点跟最后一个元素交换)
    //数组中的第一个元素是堆顶，也是最大的元素。
    //我们把它跟最后一个元素交换，那最大元素就放到了下标为n的位置
    function heapSort(&$tree, $n)
    {
        $this->buildHeap($tree, $n);
        for($i = $n-1; $i >= 0; $i--) {
            $this->swap($tree, $i, 0);
            //剩下的i个元素重新构建成堆
            $this->heapify($tree, $i, 0);
        }
    }

    /*
        递推：2,5,3,1,10,4:
        n = 6  6   6
        i = 2  1   0
        l = 5  3   1
        r = 6  4   2
        ======================     
        堆前：2,5,3,1,10,4:
               2
           5       3
        1    10  4   0
        =======================
        堆后：10.5,4,1,2,3
               10
            5        4
        1     2    3   0
    */
    function main()
    {
        /*$tree = [10, 4, 3, 5, 1, 2];
        $n = count($tree);
        $this->heapify($tree, $n, 0);*/

        $tree = [2, 5, 3, 1, 10, 4];
        $n = count($tree);
        $this->heapSort($tree, $n);

        for ($i = 0; $i < $n; $i++)
        {
            printf("%d\n", $tree[$i]);
        }
        return ;
    }
}
$heapObj = new MaxHeap();
$heapObj->main();

结果

1
2
3
4
5
10