小白上楼梯(递归设计)

小白正在上楼梯，楼梯有n阶台阶，小白一次一次可以上1阶，2阶或3阶，实现一个方法，计算小白有多少种走完楼梯的方式

思路

设n阶台阶的走法数为f(n)。

如果只有1个台阶，走法有1种（一步上1个台阶），即f(1)=1；

如果有2个台阶，走法有2种（一种是上1阶，再上1阶，另一种是一步上2阶），即f(2)=2；

如果有3个台阶，走法有4种（一种每次1阶，共一种；另一种是2+1，共两种；第三种是3，共1种），即f(3)=4；

逆向推理

当有n个台阶（n>3）时，可以这样想：

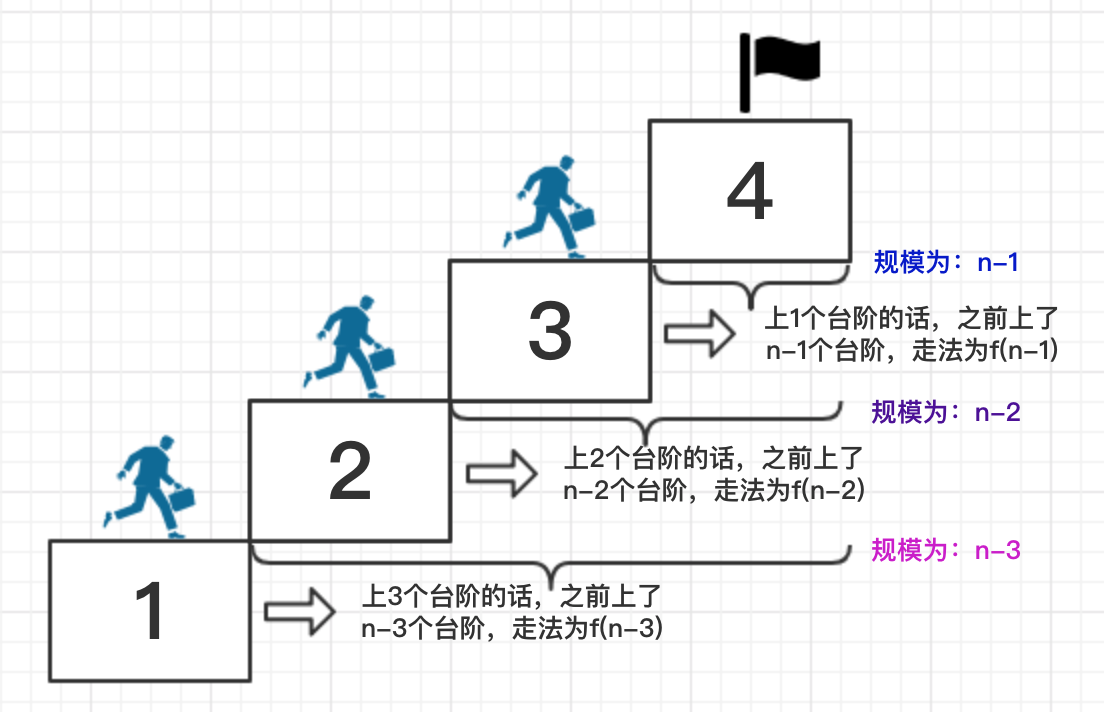
最后是一步上1个台阶的话，之前上了n-1个台阶，走法为f(n-1)种，

而最后是一步上2个台阶的话，之前上了n-2个台阶，走法为f(n-2)种，

而最后是一步上3个台阶的话，之前上了n-3个台阶，走法为f(n-3)种故而f(n)=f(n-1)+f(n-2)+f(n-3)。

列出的递归方程为：f(1)=1;f(2)=2;f(3)=4;
plt.png

结果

最后一步可能是从第n-1阶往上走1阶、从n-2阶往上走2阶，或从第n-3阶往上走3阶。因此，抵达最后一阶的走法，其实就是抵达这最后三阶的方式的总和。

关系图

小白上楼梯-递归设计

代码

function f($n) {
    if ($n == 0 || $n == 1) {
    	return 1;
    }
    if ($n == 2) {
    	return 2;
    }
    return f($n-1) + f($n-2) + f($n-3);
}

echo f(4);