斐波那契数:1、1、2、3、5、8、13、21、······前后两个数之和被称为斐波那契数。
递归:
- 递归:函数自己调用自己
- 递归的”缺陷”:会发生”栈溢出”(可以用 ulimit -s 查看linux的默认栈空间大小)
- 递归的”时间复杂度”:递归总次数*每次递归的次数
- 递归的”空间复杂度”:递归的深度*每次递归空间的大小(注意:”每次递归空间的大小”是个常数,可以基本忽略不计)递归的”深度”:树的高度(递归的过程是一个”二叉树”);
时间复杂度 O(2^n)
函数递归二叉树结构图:
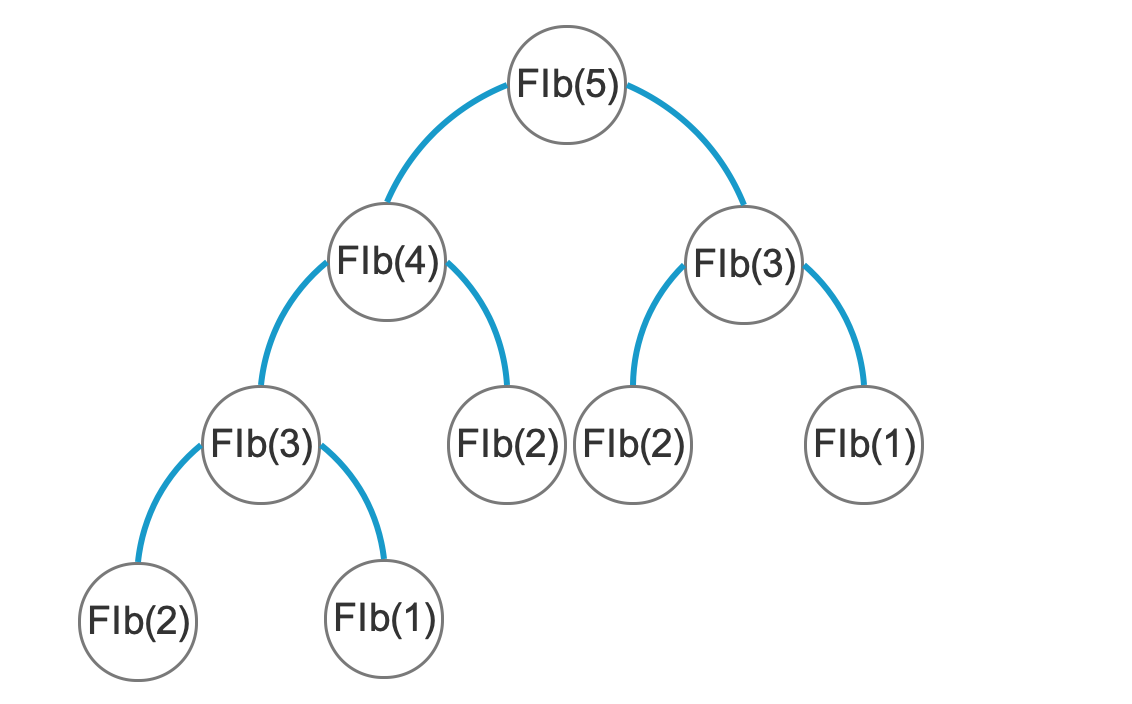
- 二叉树层数:n-1 = 5-1 = 4[当n=5时,二叉树共有4层]
- 二叉树第m层的个数:2^3 [前三层节点数= (2^3)-1=7=> (2^3)-1+2 =9]
- 二叉树总节点数:(2^(n-1)-1) 推出=> 总节点数=斐波那契数的执行次数,当n=5时,时间复杂度=O(f(5)) = O(2^3)+1,所以斐波那契数的时间复杂度 T(n) = O(f(n))=O(2^(n-2))+1 = O(2^n);
空间复杂度 O(1)
调用栈结构图:
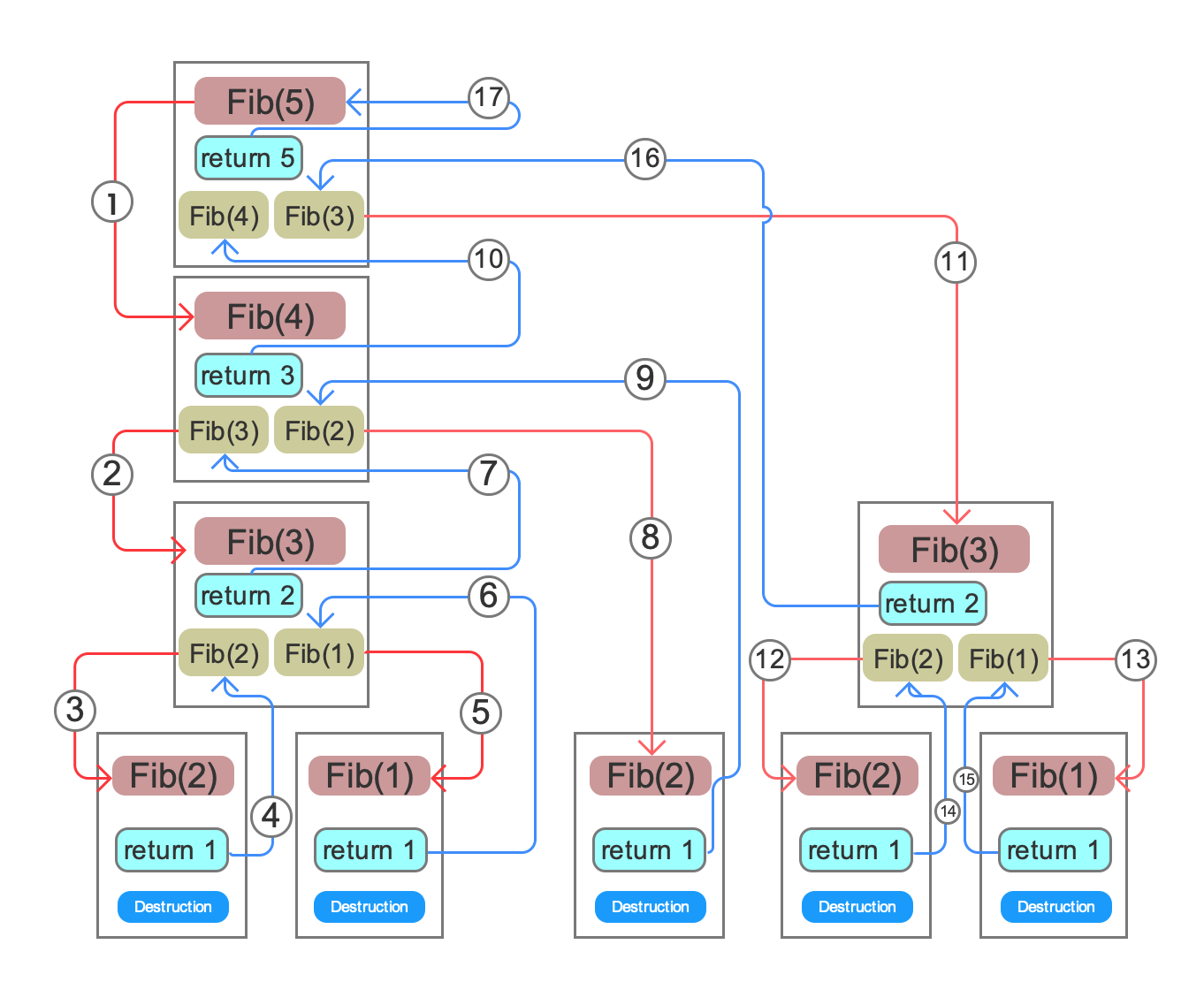
①-③ 调用顺序: Fib(5)->Fib(4)->Fib(3)->Fib(2)[返回值1]->Fib执行结束,栈空间销毁;
此时Fib(5),Fib(4),Fib(3),Fib(1)均未结束,程序共占有4个函数栈空间;④-⑩ 调用顺序: Fib(1)创建一个栈空间,调用结束后返回1,空间销毁,
此时Fib(3) = [左侧]Fib(2)+Fib(1) = 1+1 = 2,
通过第⑦步返回Fib(3)的值,第⑧步同样创建空间再次调用Fib(2),调用结束销毁空间,此时可得到Fib(4)=3,
通过第⑩步返回Fib(4)的值,此过程占用4个函数栈帧空间。⑪-⑯ 调用Fib(3),将返回值传给Fib(5),得到Fib(5)=5
整个程序执行过程中,最多占用4个函数栈帧空间的大小,设一个函数栈帧空间为C
因此可得知当n=5时,该程序空间复杂度为O(4C)=>O(1)
当求第n个斐波那契数时,程序空间复杂度为O(n-1)C (n是常数)=>O(1)
PHP代码实现:<结合步骤2看栈调用过程>
1 | line : <121-134> |
运行结果:
1 | 初始内存: 355344 字节 |
